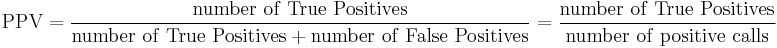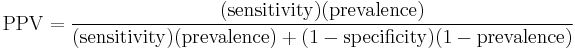Positive predictive value

In statistics and diagnostic testing, the positive predictive value, or precision rate is the proportion of subjects with positive test results who are correctly diagnosed. It is a critical measure of the performance of a diagnostic method, as it reflects the probability that a positive test reflects the underlying condition being tested for. Its value does however depend on the prevalence of the outcome of interest, which may be unknown for a particular target population. The PPV can be derived using Bayes' theorem.

Although sometimes used synonymously, a positive predictive value generally refers to what is established by control groups, while a post-test probability rather refers to a probability for an individual. Still, if the individual's pre-test probability of the target condition is the same as the prevalence in the control group used to establish the positive predictive value, the two are numerically equal.

1 Definition
2 Worked example
3 Problems with positive predictive value
- 3.1 Other individual factors
- 3.2 Different target conditions
4 See also
5 References and notes

Definition

The Positive Predictive Value is defined as

${\rm PPV} = \frac{\rm number\ of\ True\ Positives}{{\rm number\ of\ True\ Positives}%2B{\rm number\ of\ False\ Positives}} = \frac{\rm number\ of\ True\ Positives}{\rm number\ of\ positive\ calls}$

where a "true positive" is the event that the test makes a positive prediction, and the subject has a positive result under the gold standard, and a "false positive" is the event that the test makes a positive prediction, and the subject has a negative result under the gold standard.

The following diagram illustrates how the positive predictive value, negative predictive value, sensitivity, and specificity are related.

		Condition (as determined by "Gold standard")
		Condition Positive	Condition Negative
Test Outcome	Test Outcome Positive	True Positive	False Positive (Type I error)	Positive predictive value = Σ True Positive Σ Test Outcome Positive
Test Outcome	Test Outcome Negative	False Negative (Type II error)	True Negative	Negative predictive value = Σ True Negative Σ Test Outcome Negative
		Sensitivity = Σ True Positive Σ Condition Positive	Specificity = Σ True Negative Σ Condition Negative

Note that the positive and negative predictive values can only be estimated using data from a cross-sectional study or other population-based study in which valid prevalence estimates may be obtained. In contrast, the sensitivity and specificity can be estimated from case-control studies.

If the prevalence, sensitivity, and specificity are known, the positive predictive value can be obtained from the following identity:

${\rm PPV} = \frac{({\rm sensitivity}) ({\rm prevalence})}{({\rm sensitivity}) ({\rm prevalence}) %2B (1 - {\rm specificity}) (1-{\rm prevalence})}$

Worked example

Suppose the fecal occult blood (FOB) screen test is used in 2030 people to look for bowel cancer:

		Patients with bowel cancer (as confirmed on endoscopy)
		Condition Positive	Condition Negative
Fecal Occult Blood Screen Test Outcome	Test Outcome Positive	True Positive (TP) = 20	False Positive (FP) = 180	Positive predictive value = TP / (TP + FP) = 20 / (20 + 180) = 10%
Fecal Occult Blood Screen Test Outcome	Test Outcome Negative	False Negative (FN) = 10	True Negative (TN) = 1820	Negative predictive value = TN / (FN + TN) = 1820 / (10 + 1820) ≈ 99.5%
		Sensitivity = TP / (TP + FN) = 20 / (20 + 10) ≈ 67%	Specificity = TN / (FP + TN) = 1820 / (180 + 1820) = 91%

The small positive predictive value (PPV = 10%) indicates that many of the positive results from this testing procedure are false positives. Thus it will be necessary to follow up any positive result with a more reliable test to obtain a more accurate assessment as to whether cancer is present. Nevertheless, such a test may be useful if it is inexpensive and convenient.

Problems with positive predictive value

Other individual factors

Note that the PPV is not intrinsic to the test—it depends also on the prevalence [1]. PPV is directly proportional to the prevalence of the disease or condition. In the above example, if the group of people tested had included a higher proportion of people with bowel cancer, then the PPV would probably come out higher and the NPV lower. If everybody in the group had bowel cancer, the PPV would be 100% and the NPV 0%.

To overcome this problem, NPV and PPV should only be used if the ratio of the number of patients in the disease group and the number of patients in the healthy control group used to establish the NPV and PPV is equivalent to the prevalence of the diseases in the studied population, or, in case two disease groups are compared, if the ratio of the number of patients in disease group 1 and the number of patients in disease group 2 is equivalent to the ratio of the prevalences of the two diseases studied. Otherwise, positive and negative likehood ratios are more accurate than NPV and PPV, because likelihood ratios do not depend on prevalence.

When an individual being tested has a different pre-test probability of having a condition than the control groups used to establish the PPV and NPV, the PPV and NPV are generally distinguished from the positive and negative post-test probabilities, with the PPV and NPV referring to the ones established by the control groups, and the post-test probabilities referring to the ones for the tested individual (as estimated, for example, by likehood ratios). Preferably, in such cases, a large group of equivalent individuals should be studied, in order to establish separate positive and negative predictive values for use of the test in such individuals.

Different target conditions

PPV is used to indicate the probability that in case of a positive test, that the patient really has the specified disease. However there may be more than one cause for a disease and any single potential cause may not always result in the overt disease seen in a patient. There is potential to mixup related target conditions of PPV and NPV, such as interpreting the PPV or NPV of a test as having a disease, when that PPV or NPV value actually refers only to a predisposition of having that disease.

An example is the microbiological throat swab used in patients with a sore throat. Usually publications stating PPV of a throat swab are reporting on the probability that this bacteria is present in the throat, rather than that the patient is ill from the bacteria found. If presence of this bacteria always resulted in a sore throat, then the PPV would be very useful. However the bacteria may colonise individuals in a harmless way and never result in infection or disease. Sore throats occurring in these individuals is caused by other agents such as a virus. In this situation the gold standard used in the evaluation study represents only the presence of bacteria (that might be harmless) but not a causal bacterial sore throat illness. It can be proven that this problem will affect positive predictive value far more than negative predictive value. To evaluate diagnostic tests where the gold standard looks only at potential causes of disease, one may use an extension of the predictive value termed the Etiologic Predictive Value.^[1]

References and notes

Altman DG, Bland JM (9 Jul 1994). "Diagnostic tests 2: Predictive values". BMJ 309 (6947): 102. PMC 2540558. PMID 8038641. http://www.bmj.com/cgi/content/full/309/6947/102.

^ Gunnarsson RK, Lanke J (2002). "The predictive value of microbiologic diagnostic tests if asymptomatic carriers are present". Statistics in medicine 21 (12): 1773–85. doi:10.1002/sim.1119. PMID 12111911.